1. Description des méthodes eigenvals() et eigenvects()
SymPy offre des fonctionnalités pour effectuer des calculs liés aux valeurs propres (eigenvalues) et aux vecteurs propres (eigenvectors) de matrices à l'aide de la fonction eigenvals() et eigenvects().
2. Syntaxe et usage des méthodes eigenvals() et eigenvects()
Les méthodes eigenvals() et eigenvects() en SymPy sont utilisées pour calculer les valeurs propres (eigenvalues) et les vecteurs propres (eigenvectors) d'une matrice ou d'un opérateur linéaire. Voici la syntaxe et l'utilisation de ces méthodes :
Syntaxe pour utiliser eigenvals()
|
1 |
eigenvalues = matrice.eigenvals() |
Syntaxe pour utiliser eigenvects()
|
1 |
eigenvectors = matrice.eigenvects() |
3. Exemples d'usage des méthodes eigenvals() et eigenvects()
Voici comment on peut utiliser ces méthodes pour calculer les valeurs propres et les vecteurs propres d'une matrice en SymPy :
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
import sympy as sp # Définir une matrice A = sp.Matrix([[1, 1], [2, 2]]) # Calculer les valeurs propres eigenvalues = A.eigenvals() print("Valeurs propres : ", eigenvalues) # Calculer les vecteurs propres eigenvectors = A.eigenvects() print("Vecteurs propres : ", eigenvectors) """ output: Valeurs propres : {3: 1, 0: 1} Vecteurs propres : [(0, 1, [Matrix([ [-1],[ 1]])]), (3, 1, [Matrix([[1/2],[ 1]])])] """ |
- La méthode eigenvals() : renvoie un dictionnaire avec les valeurs propres comme clés et leur multiplicité comme valeurs. Dans ce cas 2 valeurs propres: 0 de multiplicité 1 et 3 de multiplicité 1
- La méthode eigenvects() : renvoie une liste de triples (valeur propre, multiplicité, vecteurs propres associés).
Remarque
En effectuant les calculs, remarquez bien que u(-1,1) et v(1/2 , 1) sont deux vecteurs propres :
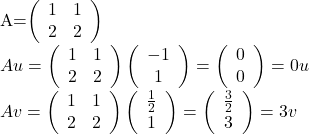
Remarque
La matrice A est diagonalisable puisqu'elle admet deux valeurs propres distinctes.
On peut aussi tester la diagonalisabilité de la matrice A à l'aide de la méthode is_diagonalizable() :
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
import sympy as sp # Définir une matrice A = sp.Matrix([[1, 1], [2, 2]]) # Vérifier si la matrice est diagonalisable if A.is_diagonalizable(): print("La matrice est diagonalisable.") else: print("La matrice n'est pas diagonalisable.") """ output: La matrice est diagonalisable. """ |
Younes Derfoufi
CRMEF OUJDA


