
- A propos de la bibliothèque Sympy
- Installation de la bibliothèque Sympy
- Les Symboles Sympy
- Les expressions de la bibliothèque Sympy
- Opération sur les expressions de la bibliothèque Sympy
- Traitement des nombres rationnels avec Sympy
- Résoudre les équations avec la bibliothèque Sympy
- Calcul intégrale avec la bibliothèque Sympy
- Calcul des dérivées avec la bibliothèque Sympy
- Calcul matriciel avec Sympy
- Liste des méthodes associées à la bibliothèque Sympy
- Liste des sous modules de la bibliothèque sympy
1. A propos de la bibliothèque Sympy
SymPy est une bibliothèque Python open-source déstinée au calcul symbolique, gratuite et est distribuée sous la nouvelle licence BSD. Elle offre des méthodes efficaces pour le calcul scientifique et elle couvre presque tous les domaines de mathématiques, analyse, algèbre linéaire et générale, géométrie, statistiques... SymPy est simple à installer et à inspecter car elle est entièrement écrite en Python avec peu de dépendances. Cette facilité d'accès combinée à une base de code simple et extensible dans un langage bien connu font de SymPy un système de calcul formel lympide et puissant. Actuellement, le noyau de la bibliothèque SymPy englobe environ 260 000 lignes de code.
2. Installation de La bibliothèque SymPy
La bibliothèque Sympy rapidement en toute aisance via l'utilitaire pip avec la commande :
|
1 |
pip install sympy |

Pour vérifier la version de Sympy installée, on utilise le code suivant:
|
1 2 3 |
>>> import sympy >>> sympy.__version__ '1.10.1' |
3. Les symbols Sympy
La bibliothèque SymPy peut être utilisé dans n'importe quel environnement où Python est disponible. Afin de pouvoir l'utiliser, nous devons préalablement l'importer:
|
1 |
>>> from sympy import * |
Pour définir un symbol x , on utilise la commande:
|
1 2 3 |
>>> x = Symbol('x') # notez le S en majuscule >>> x x |
On peut aussi utiliser la syntaxe:
|
1 2 3 4 |
>>> import sympy as sy >>> x = sy.Symbol('x') >>> x x |
Pour définir plusieurs symbols Sympy en même temps, on utilise la commande:
|
1 2 3 |
>>> x, y, z = symbols('x y z') # notez le 's' en minuscule >>> x, y, z ( x , y , z ) |
4. Les expressions sympy
Une expression sympy n'est autre qu'une combinaison de symbols à l'aides des opérations classiques de mathématiques comme l'addition, multiplication...
Exemple
|
1 2 3 4 5 6 7 8 9 |
import sympy as sy x= sy.Symbol('x') y = sy.Symbol('y') # on defint une expression exp = x*sy.sin(y) + y*sy.sin(x) print(exp) # affiche: x*sin(y) + y*sin(x) |
5. Opération sur les expressions sympy
On peut aussi faire des opérations sur les expressions comme factorisation, développement, symplification...
5.1 Développer une expression sympy à l'aide de la méthode expand()
La méthode expand() comme tous les autres langages de calcul symbolique, permet de développer une expression mathématique
Exemple (développer une expression à l'aide de la méthode expand() )
|
1 2 3 4 5 6 7 |
import sympy as sy x = sy.Symbol('x') y = sy.Symbol('y') expr = (x - y)**3 print(expr.expand()) # affiche: x**3 - 3*x**2*y + 3*x*y**2 - y**3 |
5.2 Simplification
La bibliothèque sympy est dotée de la méthode simplify() qui permet de simplifier une expression mathématique:
Exemple( simplifier une expression via la méthode simplify() )
|
1 2 3 4 5 6 7 8 |
import sympy as sy x = sy.Symbol('x') expr1 = (x + 1)**2 expr2 = x**2 + 2*x + 1 expr3 = sy.simplify( expr2 - expr1 ) print("expr2 - expr1 = " , expr3 ) # affiche: expr2 - expr1 = 0 |
5.3 Substitution des symbols dans sympy
Dans une expression sympy, on peut substituer un symbol par une valeur numérique ou par un autre grâce à la méthode subs().
Exemple(substitution d'un symbol par une valeur numérique )
|
1 2 3 4 5 6 7 8 |
import sympy as sy x = sy.Symbol('x') expr = x**2 + x + 3 # substitution de x par 1 print(expr.subs(x , 1)) # affiche 5 |
Exemple(substitution d'un symbol par un autre symbol)
|
1 2 3 4 5 6 7 8 9 |
import sympy as sy x = sy.Symbol('x') y = sy.Symbol('y') expr = x**2 + x*y + 3*x + y # substitution de x par y ( remplacement de x par y) print(expr.subs(x , y)) # affiche: 2*y**2 + 4*y |
5.4 Evalution d'une expression sympy
Pour évaluer une expression, sympy nous offre la méthode evalf()
Pour bien comprendre le mécanisme de fonctionnement de cette méthode essayons d'examiner l'affichage du nombre pi
Exemple
from sympy import pi
|
1 |
print(pi) # affiche: pi |
Comme vous l'avez remarqué, l'exemple ci-dessus ne nous permet pas d'obtenir la valeur de pi et c'est grâce à la méthode evalf() qu'on peut l'obtenir.
Exemple
|
1 2 3 4 5 6 7 8 9 10 11 |
from sympy import pi # Default value of pi print(pi.evalf()) # affiche: 3.14159265358979 # get value of pi with 3 decimal numbers print(pi.evalf(3))# affiche: 3.14 # get value of pi with 5 decimal numbers print(pi.evalf(5)) # affiche: 3.1416 |
5.5 transformer une expression sympy en une fonction
Une expression sympy par défaut ne peut jouer le rôle d'une fonction mathématique, mais elle le peut à l'aide de la méthode lambdify()
Syntaxe
|
1 |
f = lambdify(symbol , expression) |
Exemple
|
1 2 3 4 5 6 7 8 |
import sympy as sy x = sy.Symbol('x') expr = x**2 + 3*x + 5 f = sy.lambdify(x , expr) print("f(0) = " , f(0)) # affiche: f(0) = 5 |
5.6 Factoriser une expression à l'aide de la méthode sympy.factor()
A l'aide de la méthode sympy.factor(), vous pouvez factoriser toute expressions mathématiques via la syntaxe
Syntaxe
|
1 |
sympy.factor(expression) |
Exemple (factorisation d'un polynome)
|
1 2 3 4 5 6 7 8 9 |
import sympy as sy # création du symbol x x = sy.Symbol('x') P = x**2 - 2*x + 1 fact = sy.factor(P) print(fact) # affiche: (x - 1)**2 |
5.7 Code LaTeX d'une expression sympy
Le code LaTeX d'une expression sympy s'obtient facilement à l'aide de la méthode latex()
Exemple
|
1 2 3 4 5 6 |
from sympy import * x = Symbol('x') I = Integral(sin(x) , x) print(latex(I)) # affiche: \int \sin{\left(x \right)}\, dx |
6. Traitement des nombres rationnels avec sympy
Afin de pouvoir gérer et manipuler des nombres rationnels sous forme de fractions a/b , sympy nous offre la classe Rational qui permet de réaliser l'affaire:
Exemple (création d'un nombre rationnel )
|
1 2 3 4 5 |
import sympy as sy r = sy.Rational(3, 7) print("la valeur de r est r = " , r) # affiche: r = 3/7 |
On peut aussi effectuer des opérations sur les nombres rationnels avec sympy
Exemple (somme et produit de deux rationnels)
|
1 2 3 4 5 6 7 8 |
import sympy as sy r1 = sy.Rational(1, 3) r2 = sy.Rational(1, 2) s = r1 + r2 p = r1*r2 print("La somme est r1 + r2 = " , s) # affiche: La somme est r1 + r2 = 5/6 print("La produit est r1 x r2 = " , p) # affiche: La produit est r1 x r2 = 1/6 |
Exemple(transformation d'un nombre décimal en fraction)
|
1 2 3 4 |
import sympy as sy r = 1.25 print(sy.Rational(r)) # affiche 5/4 |
7. Résoudre les équations en Python avec la méthode sympy.solve()
Avec l'aide de la méthode sympy.solve(expression), vous pouvez résoudre facilement les équations mathématiques. Cette méthode renverra la liste des racines de l'équation qui est fournie comme paramètre en utilisant la méthode sympy.solve().
Syntaxe
|
1 |
sympy.solve(expression) |
Exemple
|
1 2 3 4 5 6 |
import sympy as sy x = sy.Symbol('x') # resoudre l'équation: x**2 - 3 = 0 print(sy.solve(sy.Eq(x**2 , 3))) # affiche: [-sqrt(3), sqrt(3)] |
Remarque
On peut aussi résoudre un système d'équations en utilisant la syntaxe:
|
1 |
sy.solve( (eq1 , eq2,eq3) , (x1,x2,x3,...) |
Nous allons à titre d'exemple résoudre le système:
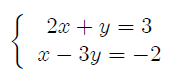
|
1 2 3 4 5 6 7 8 9 10 11 12 |
import sympy as sy x = sy.Symbol('x') y = sy.Symbol('y') # définir le système d'équations eq1 = sy.Eq(2*x + y , 3) eq2 = sy.Eq(x - 3*y , -2) # resoudre le système d'équation solution = sy.solve( (eq1 , eq2) , (x,y) ) print( solution ) # affiche: {x: 1, y: 1} |
8. Calcul Intégrale avec Sympy Python
Le package SymPy contient le module de calcul intégrale. Il implémente des méthodes pour calculer les intégrales définies et indéfinies des expressions mathématiques. La méthode integrate() est utilisée pour calculer les intégrales définies et indéfinies.
Pour calculer une intégrale indéfinie ou primitive, il suffit de passer la variable après l'expression dans la méthode integrate().
Syntaxe
|
1 |
primitive_expression(x) = sy.integrate( expression , x) |
Exemple
|
1 2 3 4 5 6 7 8 |
import sympy as sy x = sy.Symbol('x') expr = x**2 + 3*x + 5 # calcul de la primitive primitive = sy.integrate(expr , x) print(primitive) # affiche: x**3/3 + 3*x**2/2 + 5*x |
9. Differentiation des fonctions à l'aide de la méthode diff()
La bibliothèque sympy permet aussi de calculer la dérivée d'une expression grâce à la méthode diff().
Syntaxe
|
1 |
derivativeof_expression = sympy.diff(expression , symbol) |
Exemple
|
1 2 3 4 5 6 7 8 |
import sympy as sy x = sy.Symbol('x') expr = x**5 # drivative function derivative = sy.diff(expr , x) print(derivative) # affiche: 5*x**4 |
La même méthode diff() permet de calculer les dérivées succéssives d'une expression
Exemple
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
import sympy as sy x = sy.Symbol('x') expr = x**5 # drivative derivative1 = sy.diff(expr , x) print(derivative1) # affiche: 5*x**4 # second derivative derivative2 = sy.diff(expr , x , 2) print(derivative2) # affiche: 20*x**3 #3rd order derivative derivative3 = sy.diff(expr , x , 3) print(derivative3) # affiche: 60*x**2 |
10. Calcul matriciel avec sympy
10.1 A propos des matrices sympy
En mathématiques, une matrice (matrix en anglais) est un tableau à deux dimensions constitué de nombres, de symboles ou d'expressions.Il contient des données stockées dans les lignes et les colonnes du tableau. Dans une matrice Python, les séries horizontales d'éléments sont appelées "lignes", tandis que les séries verticales d'éléments sont appelées "colonnes".
Le package SymPy possède un module nommé matrix qui traite complètement la gestion des matrices. Il inclut la classe Matrix dont l'objet représente une matrice.
Afin de pouvoir utiliser le module matrix, vous devez au préalable importer la classe Matrix via la commande:
|
1 |
from sympy.matrices import Matrix |
Exemple ( création d'une matrice 2x2)
|
1 2 3 4 5 6 |
from sympy import Matrix # création d'une matrice du type 2x2 A = Matrix([[1, 2], [1, 1] ]) |
10.2 Opération basiques sur les matrices sympy
10.2.1 Les propriétés shape, rows et cols
Pour connaitre le type d'une matrice sympy, le nombre de lignes et de colonnes, on utilise lespropriétés: shap, rows et cols
- shape: détermine le type de la matrice 'mxn'
- rows: renvoie le nombre de lignes de la matrice
- cols: renvoie le nombre de colonnes de la matrice
Exemple
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
from sympy import Matrix A = Matrix([[1, 2], [1, 1], [3, -1], ]) Type = A.shape lignes = A.rows colonnes = A.cols print("Type de la matrice : " , Type) # affiche: Type de la matrice : (3, 2) print("Nombre de lignes de la matrice : " , lignes) # affiche: Nombre de lignes de la matrice : 3 print("Nombre de colonnes de la matrice : " , colonnes) # affiche: Nombre de colonnes de la matrice : 2 |
10.2.2 Accéder aux lignes et aux colonnes d'une matrice sympy
Pour obtenir une ligne ou une colonne d'une matrice A, on utilise row ou col. Par exemple, A.row(0) obtiendra la première ligne. A.col(-1) obtiendra la dernière colonne.
Exemple
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
from sympy import Matrix A = Matrix([[1, 2], [1, 1], [3, -1], ]) print("Première ligne :" , A.row(0)) # affiche: Première ligne : Matrix([[1, 2]]) print("Dernière ligne : " , A.row(-1)) # affiche: Dernière ligne : Matrix([[3, -1]]) print("Première colonne : " , A.col(0)) # affiche: Première colonne : Matrix([[1], [1], [3]]) |
9.2.3 Insertion des lignes et des colonnes
Pour insérer des lignes ou des colonnes dans une matrice sympy, on utilise les méthodes row_insert() ou col_insert().
Exemple
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
from sympy import Matrix A = Matrix([[1, 2], [1, 1], [3, -1], ]) # insertion d'une ligne à la position d'index = 1 A1 = A.row_insert(1, Matrix([[5, 3]])) print("A1 = " , A1) # affiche: A1 = Matrix([[1, 2], [5, 3], [1, 1], [3, -1]]) # insertion d'une colonne à la position d'index = 2 A2 = A.col_insert(2 , Matrix([11, 13 , 77])) print("A2 = " , A2) # affiche: A2 = Matrix([[1, 2, 11], [1, 1, 13], [3, -1, 77]]) |
10.3 Déterminant d'une matrice avec sympy
Pour calculer le déterminant d'une matrice sympy, on utilise la méthode det()
Exemple
|
1 2 3 4 5 6 |
from sympy import Matrix A = Matrix([[1, 2], [1, 1] ]) print(A.det()) # affiche -1 |
On peut aussi calculer le déterminant d'une matrice sympy définie à l'aide des symbols
Exemple
|
1 2 3 4 5 6 7 |
from sympy import Matrix , symbols x , y , z , t = symbols('x y z t') B = Matrix([[x, z], [y, t] ]) print(B.det()) # t*x - y*z |
10.4 Valeurs propres, vecteurs propres et diagonalisation d'une matrice sympy
10.4.1 Valeurs propres d'une matrice sympy
Pour trouver les valeurs propres d'une matrice sympy, on utilise la méthode eigenvals(). eigenvals renvoie un dictionnaire de paires eigenvalue: algebraic_multiplicity.
Exemple
|
1 2 3 4 5 6 7 8 |
from sympy import Matrix A = Matrix([[2, 2, -2], [0, 1, 1], [0, -2, 4] ]) print(A.eigenvals()) # affiche: {3: 1, 2: 2} |
L'exemple ci-dessus montre que la matrice A possède deux valeurs propres: 3 de multiplicité 1 et 2 de multiplicité 2.
10.4.2 Vecteurs propres d'une matrice sympy
Pour trouver les vecteurs propres d'une matrice, on utilise la méthode eigenvects(). eigenvects renvoie une liste de tuples de la forme (eigenvalue, algebraic_multiplicity, [eigenvectors]).
Exemple
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
from sympy import Matrix A = Matrix([[2, 2, -2], [0, 1, 1], [0, -2, 4] ]) print(A.eigenvects()) """ affiche [(2, 2, [Matrix([[1], [0], [0]]), Matrix([[0], [1], [1]])]), (3, 1, [Matrix([[ -1], [1/2], [1]])] )] """ |
11. Liste des méthodes associées à la bibliothèque Sympy
- Abs() : Pour calculer la valeur absolue d'une expression.
- accumulate(): Pour effectuer une accumulation sur une séquence.
- acosh(), asinh(), et atanh() : Pour calculer les fonctions trigonométriques hyperboliques inverses.
- add() et Mul() : Créer des expressions en additionnant et ou multipliant des expressions mathématiques.
- airyai() et airybi(): Pour calculer les fonctions d'Airy.
- apart() : Pour effectuer une décomposition en éléments simples.
- asin(), acos(), et atan() : Pour calculer les fonctions trigonométriques inverses.
- bernoulli() et euler() : Pour accéder aux nombres de Bernoulli et aux nombres d'Euler.
- besseli() et besselk(): Pour calculer les fonctions de Bessel modifiées.
- binomial() : Pour calculer les coefficients binomiaux.
- cos(), sin(), tan(), etc. : Pour calculer des fonctions trigonométriques.
- cot() : Pour calculer la cotangente d'une expression.
- count_atoms(): Pour compter le nombre total de symboles atomiques dans une expression.
- count_ops(): Pour compter le nombre total d'opérations dans une expression.
- Derivative() : Pour calculer des dérivées.
- diff(): Pour calculer la dérivée d'une expression par rapport à une variable.
- dirichlet_eta(): Pour calculer la fonction eta de Dirichlet.
- divisors(): Pour obtenir la liste des diviseurs d'un nombre.
- Ei(): Pour calculer l'intégrale exponentielle.
- eigenvals() et eigenvects() : Pour calculer les valeurs propres et les vecteurs propres d'une matrice.
- elliptic_e() et elliptic_k(): Pour calculer les fonctions elliptiques complètes..
- Eq(): Pour représenter une équation symbolique.
- exp() : Pour calculer l'exponentielle d'une expression..
- expand() : Pour développer une expression symbolique.
- factor() : Pour factoriser une expression symbolique.
- floor() et ceiling() : Pour calculer les fonctions plancher et plafond d'une expression.
- Fourier() : Pour effectuer une transformation de Fourier.
- FresnelS() et FresnelC(): Pour calculer les intégrales de Fresnel.
- Function() : Pour définir des fonctions symboliques.
- gamma() : Pour calculer la fonction gamma.
- gcd() et lcm(): Pour calculer le plus grand commun diviseur (PGCD) et le plus petit commun multiple (PPCM) de plusieurs nombres.
- Heaviside(): Pour représenter la fonction de Heaviside.
- Hermite() : Pour calculer les polynômes d'Hermite.
- hyper(): Pour représenter des fonctions hypergéométriques.
- Integral() : Pour représenter une intégrale définie.
- integrate() : Pour calculer l'intégrale d'une expression par rapport à une variable.
- inverse_fourier_transform() : Pour effectuer une transformation de Fourier inverse.
- inverse_laplace_transform() : Pour effectuer une transformation de Laplace inverse.
- is_prime(): Pour vérifier si un nombre est premier.
- Jacobi() : Pour représenter les fonctions jacobiennes.
- KroneckerDelta(): Pour représenter le delta de Kronecker.
- lambdify(): Pour créer une fonction numérique à partir d'une expression SymPy.
- laplace_transform() : Pour effectuer une transformation de Laplace.
- legendre() : Pour calculer les polynômes de Legendre.
- LegendrePoly(): Pour représenter les polynômes de Legendre associés.
- limit() : Pour calculer une limite d'une expression.
- limit_seq() (avec des séquences récursives): Pour calculer la limite d'une séquence récursive.
- linear_eq_to_matrix() : Pour transformer un système d'équations linéaires en matrices.
- linsolve(): Pour résoudre des systèmes d'équations linéaires.
- log() : Pour calculer le logarithme de base arbitraire d'une expression.
- Matrix(): Pour créer des matrices symboliques.
- matrix_symbols(): Pour générer des symboles matriciels.
- meijerg(): Pour représenter les fonctions de Meijer.
- Min() et Max(): Pour calculer le minimum et le maximum de plusieurs expressions.
- N() : Pour évaluer une expression symbolique numériquement.
- next_poly() et prev_poly(): Pour obtenir le prochain ou le précédent polynôme d'une certaine forme.
- nextprime(): Pour trouver le prochain nombre premier après un nombre donné.
- nonlinsolve(): Pour résoudre des systèmes d'équations non linéaires.
- Not() : Pour représenter une négation logique.
- Or() et And() : Pour représenter des opérations logiques OR et AND.
- pi et E: Pour accéder aux constantes mathématiques π (pi) et e (la base du logarithme naturel).
- Piecewise(): Pour définir une fonction par morceaux.
- Poly(): Pour manipuler des polynômes.
- polygamma(): Pour calculer les fonctions polygammes.
- prevprime(): Pour trouver le nombre premier précédent avant un nombre donné.
- Product() : Pour représenter un produit explicite.
- Rational() : Pour créer des nombres rationnels à partir d'expressions fractionnaires.
- re(), im(), arg(), et abs(): Pour extraire différentes parties d'une expression complexe.
- RootOf(): Pour représenter des racines d'équations polynomiales.
- satisfiable() (avec des expressions booléennes): Pour vérifier si une expression booléenne est satisfaisable.
- sec() et csc() : Pour calculer la sécante et la cosécante d'une expression.
- simplify() : Pour simplifier une expression symbolique autant que possible.
- simplify_logic() (avec des expressions booléennes): Pour simplifier des expressions logiques booléennes.
- simplify_rational() : Pour simplifier des expressions rationnelles.
- SingularFunction(): Pour représenter les fonctions singulières.
- solve() : Pour résoudre des équations symboliques.
- solve_linear_system() : Pour résoudre un système d'équations linéaires.
- solve_univariate_inequality(): Pour résoudre des inégalités univariées.
- solveset(): Pour résoudre des équations symboliques avec des solutions réelles ou complexes.
- spherical_besseljn() : Pour calculer les fonctions de Bessel sphériques.
- sqrt() : Pour calculer la racine carrée d'une expression.
- Subfactorial(): Pour calculer le sous-factoriel d'un nombre.
- subs(): Pour substituer des valeurs dans une expression symbolique.
- Sum() : Pour représenter une sommation explicite.
- summation(): Pour effectuer une sommation.
- tan() : Pour calculer la tangente d'une expression.
- together() : Pour combiner des fractions.
- trigsimp() : Pour simplifier des expressions trigonométriques.
- Ynm(): Pour représenter les harmoniques sphériques.
- zeta(): Pour calculer la fonction zêta de Riemann.
- symbols(): Pour définir des symboles symboliques.
12. Liste des sous modules de la bibliothèque sympy
SymPy est une bibliothèque Python de calcul symbolique puissante qui offre de nombreux sous-modules pour effectuer une variété de tâches mathématiques. Ces sous-modules de SymPy couvrent une vaste gamme de domaines mathématiques et scientifiques, ce qui en fait une bibliothèque polyvalente pour le calcul symbolique en Python. Vous pouvez importer les sous-modules dont vous avez besoin pour résoudre des problèmes spécifiques.
Voici une liste des principaux sous-modules de SymPy :
- sympy.core : Ce module contient les éléments fondamentaux de SymPy, tels que les objets symboliques, les expressions symboliques et les fonctions mathématiques de base.
- sympy.solvers : Ce module contient des solveurs pour résoudre des équations algébriques, différentielles, et autres, y compris solve, dsolve, solve_univariate_inequality, etc.
- sympy.calculus : Ce module propose des outils pour effectuer des calculs différentiels et intégraux, notamment diff, integrate, et d'autres.
- sympy.series : Vous pouvez utiliser ce module pour travailler avec des séries de Taylor, des développements en série, et d'autres opérations liées aux séries.
- sympy.matrices : Ce module permet la manipulation de matrices, la résolution de systèmes d'équations linéaires et la réalisation d'opérations matricielles.
- sympy.geometry : Ce module fournit des fonctionnalités pour la géométrie, telles que la création de points, de lignes, de cercles, de polygones, et la résolution de problèmes géométriques.
- sympy.physics : Ce sous-module propose des fonctionnalités pour la physique, notamment la mécanique quantique, la mécanique classique, et d'autres domaines de la physique.
- sympy.stats : Vous pouvez l'utiliser pour effectuer des calculs statistiques, notamment la création de distributions de probabilité, le calcul d'espérance, de variance, et d'autres statistiques.
- sympy.combinatorics : Ce module est destiné à la combinatorique, offrant des outils pour travailler avec les permutations, les combinaisons, et d'autres structures combinatoires.
- sympy.logic : Ce module est utilisé pour travailler avec la logique symbolique, notamment la manipulation d'expressions booléennes, la simplification d'expressions logiques, etc.
- sympy.sets : Il fournit des fonctionnalités pour travailler avec les ensembles mathématiques, notamment l'union, l'intersection, la différence, etc.
- sympy.functions : Ce module contient une variété de fonctions utilisées en calcul symbolique mathématique.
- sympy.ntheory : Vous pouvez l'utiliser pour effectuer des calculs liés à la théorie des nombres, tels que la factorisation, les tests de primalité, la recherche de diviseurs, etc.
- sympy.parsing : Ce sous-module offre des fonctionnalités de conversion entre expressions textuelles et objets SymPy.
- sympy.printing : Il permet de formater et d'imprimer des expressions SymPy dans divers formats, tels que LaTeX, Unicode, etc.
Younes Derfoufi
CRMEF OUJDA


