1. Description de l'apprentissage profond

Avec les progrès rapides dans le domaine de l'intelligence artificielle, nous voyons diverses technologies effrayantes qui s'explosent en peu de temps. Et quand on parle d'apprentissage en profondeur, on parle de réseaux de neurones. Mais la question demeure, comment puis-je suivre tous ces changements dans ce domaine ? Par où va t-on commencer? Par exemple, nous voyons différents réseaux de neurones de CNN, RNN, LSTM et bien sûr d'autres réseaux. L'un des principaux obstacles qui entravent la créativité dans le domaine de l'apprentissage en profondeur est votre application du côté pratique sans une compréhension suffisante de la partie théorique et mathématique. Le sujet est plus facile que vous ne l'imaginez, on n'exagère pas si on vous dis que si vous comprenez la base dans ce tutoriel, il vous sera plus facile de comprendre n'importe quel sujet en apprentissage profond car la base est la même.
L'apprentissage profond, ou ("Deep Learning" en anglais), est une branche de l'intelligence artificielle qui s'appuie sur des modèles de réseaux de neurones artificiels pour apprendre à partir de données. L'objectif est de créer des modèles capables de prendre des décisions ou d'effectuer des prédictions en se basant sur des données d'entrée, telles que des images, du texte, des signaux audio ou des séries temporelles...

Le terme "profond" fait référence à la profondeur des réseaux de neurones utilisés dans l'apprentissage profond. Contrairement aux réseaux de neurones classiques, qui ont une ou deux couches de neurones intermédiaires, les réseaux de neurones profonds peuvent en avoir des dizaines de couches cachées.
Les applications de l'apprentissage profond sont nombreuses et en constante expansion, allant de la reconnaissance d'images et de la détection de fraudes à la prédiction de maladies et à la création de voix synthétiques.

2. La structure des systèmes basés sur les réseaux de neurones

Les systèmes neuronaux d'apprentissage profond consistent en un groupe connecté de neurones qui sont organisés au sein d'un ensemble de couches, comme suit :

1. Couche d'entrée : cette couche est responsable de la réception des données d'entrée (données initiales) et de leur préparation pour le traitement dans les couches neurales qui la suivent.
2. Couche cachée : Cette couche existe entre la couche d'entrée et la couche de sortie, où les unités neuronales calculent les poids totaux des entrées puis les préparent pour la couche suivante grâce à des fonctions d'activation. .
3. Couche de sortie : C'est la dernière couche du réseau et elle est chargée de donner les résultats.

3. Types de réseaux de neurones artificiels

La plupart des réseaux de neurones qui existent actuellement dépendent de l'idée de base, qui est le perceptron. Voyons ce qu'est l'idée d'un perceptron
Perceptron : C'est l'un des modèles les plus anciens et les plus simples des réseaux de neurones artificiels. Il est utilisé comme classificateur linéaire pour prédire et classer deux objets binaires différents, comme on peut le voir sur l'image de gauche ci-dessous:

Le premier point auquel nous réfléchissons avant de penser à la conception du modèle est quel est l'objectif? ou le problème qu'on essaie de résoudre? à t-on- les données ? Ok, supposons que nous ayons une base de données contenant des photos de chats et de chiens. Notre problème que nous essayons de résoudre est que nous voulons concevoir un modèle capable de classer toute image que je donne au modèle et nous dit qu'il s'agit, par exemple, d'un chat ou d'un chien. D'ACCORD? Après avoir compris ce qui est requis et quel est notre problème que nous essayons de résoudre, permettez-moi maintenant d'élaborer davantage sur la question.

La première question qui vous vient à l'esprit est comment le modèle fait-il la distinction entre les deux images ?

Cela se fait automatiquement dans les couches cachées, et nous verrons dans les prochains articles comment le processus se fait en détail. Mais le point important que vous devez savoir maintenant est que les données des images de chats et de chiens que nous avons supposées être présentes avec nous doivent être associées à des étiquettes. Que voulez-vous dire? En bref, cela signifie que chaque image de chat a une colonne vectorielle en face qui contient ou montre que cette image que vous voyez comme une image de chat, et c'est ce que nous appelons une étiquette. Même chose pour les chiens.

4. Conception du modèle de classification

Pourquoi avons-nous besoin de cette étape ?

Nous en avons besoin car le modèle que nous construirons éventuellement est une machine. Par conséquent, nous devons lui dire pendant la phase d'entraînement que vous voyez cette image qui vous est venue comme une entrée, vous la voyez comme une image de chat, et ainsi de suite. Qu'en est-il de la phase de test ? Ce que nous devons dire au modèle, c'est que l'image est une image de chat, car c'est ce que nous attendons du modèle. Pendant la période de test, nous lui donnons simplement l'image, et le modèle nous attend et nous dit que vous voyez l'étiquette ou cette image que vous voyez comme une image de chat basée sur les images sur lesquelles il s'est entraîné pendant la période d'entraînement. Les étiquettes sont généralement des nombres, comme zéro pour un chat, un pour un chien, etc.
Ok, maintenant tout ce que nous avons à faire est de donner les données au modèle, et à travers les couches cachées, il reconnaîtra les images et distinguera l'image du chat du chien. Bien sûr, les images de chats ont des caractéristiques différentes des caractéristiques du chien, et ce modèle apprendra de lui-même, et nous verrons comment dans les prochains articles. Remarque : La différence entre le deep learning et le machine learning est qu'en deep learning, le modèle extrait les propriétés par lui-même, tandis qu'en machine learning, nous définissons nous-mêmes les propriétés.

Comment concevons-nous notre propre modèle de classification des chats ou des chiens ?

Regardez l'image de gauche dans l'image N°1 et considérez les points bleus pour représenter les chats et les points orange pour représenter les chiens. Il peut vous venir à l'esprit, comment régler ce modèle afin de classer les données, que si le point est bleu, cela signifie un chat, et si le point est orange, cela signifie un chien ? Quelle est la différence entre les deux images ci-dessus ??
La différence est que l'image de gauche contient des données pour les chats et les chiens, mais nous voyons que les données sont distribuées linéairement. Que voulez-vous dire? Je veux dire que si les données sont linéaires, cela signifie qu'il est facile de tracer une ligne droite ou oblique séparant les points bleu et orange, mais si les données ne sont pas distribuées de manière linéaire comme on le voit sur l'image de droite de la figure 1 , ici nous devons tracer une ligne en zigzag afin de différencier les points bleus et orange Ainsi, cela signifie que les données sont distribuées de manière non linéaire.

Que représente la ligne sur le dessin ?

La ligne dans le dessin est le modèle que nous voulons construire, car notre objectif est de savoir différencier les chats et les chiens, n'est-ce pas ? Si nous proposons une nouvelle image dans la phase de test, le Moodle n'a pas vu cette image auparavant. Le modèle trouve l'image et trouve ses propriétés, puis en fonction des propriétés de l'image, le modèle détermine si les propriétés indiquent que l'image est un chat ou un chien. Si nous supposons que l'image est une image de chat et que le modèle la lit correctement. Ainsi, l'image sera classée comme un chat, et l'image sera également sous la forme d'un point, à côté des points bleus qui représentent les chats, et ainsi de suite.
Revenons au perceptron. Le perceptron ne traite que des données linéairement séparables comme l'image de gauche, et le modèle que nous allons construire est la ligne dans l'image de gauche de la figure 1. Quant à l'image de droite, le Perceptron ne peut pas le gérer et nous devons utiliser des réseaux plus avancés, tels que CNN et autres. Ok, le modèle que nous allons construire est la ligne que nous voyons sur l'image 1 à gauche. Comment c'est? Parce que le but de notre dressage de modèles est de séparer les chats des chiens. Dans le cas où nous aurions besoin de nouvelles données, le modèle sera construit sous la forme d'une ligne, et donc les nouvelles données seront comparées à la ligne, qui est le modèle. Si au-dessus de la ligne, cela signifie des chats, et si en dessous de la ligne, cela signifie des chiens, et ainsi de suite.

La question importante est, que signifie la ligne mathématiquement ?

en algèbre et équations. La ligne dans le dessin représente l'équation linéaire suivante : y = w * x + b. Je peux expliquer ces détails mathématiques dans un article séparé. Comment cette équation représente-t-elle la ligne, mais pour l'instant, assurez-vous de l'information que la ligne dans l'image de gauche dans l'image numéro 1 représente cette équation.
Nous avons mentionné il y a quelque temps que nous allons simplement donner au modèle des données et des étiquettes, et cela se fait dans la couche d'entrée, et il réapprend, n'est-ce pas ? Le X ici est la donnée dans la base de données, qui dans notre exemple est l'image des chats et des chiens, et ces images contiennent les caractéristiques. Ok, donc x dans l'équation est connu, mais y et b nous sont inconnus.

Ok, maintenant comment répondre à la valeur de w et b ? Que signifie leur valeur pour nous ?

Premièrement, w représente des poids ou ce qu'on appelle des paramètres, et ces valeurs sont très importantes pour apprendre et connaître leurs valeurs. Pourquoi? Parce que la valeur du poids d'apprentissage w ou ce qu'on appelle les paramètres est très importante, car pendant la période d'entraînement, le modèle essaiera d'apprendre ces valeurs et de les garder proches des valeurs de propriétés, par exemple, des images de chats ou des photos de chiens. Que signifie cette proximité ? Cela signifie que nous essayons de trouver la valeur des poids qui permettent au modèle de réduire le pourcentage d'erreur entre ce qu'il attend et l'image réelle, par exemple l'image du chat. Ainsi, connaître ces valeurs permet au Moodle de savoir quelles propriétés appartiennent aux images de chat ou aux images de chien. Par conséquent, si nous apportons une nouvelle image, il saura comment la classer. Ok, maintenant comment apprenons-nous ces valeurs ? J'ai deux options : la première est que nous nous asseyions et essayions nos numéros sans fin, et nous pourrions trouver une solution, ou non.

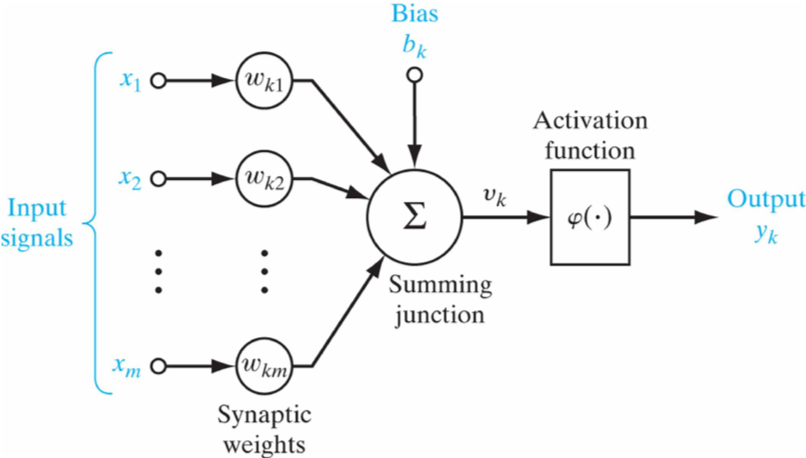
Signification mathématique:

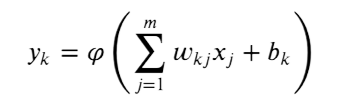
La structure générale n'est-elle pas claire? Et aussi l'équation mathématique ?

Et bien le truc est beaucoup plus facile que vous ne le croyez. Premièrement, l'équation linéaire est la même équation que celle que nous avons mentionnée dans notre exemple précédent, mais la différence réside dans le signe plus et l'activation, et nous verrons ce que c'est.

A- Qu'est-ce que je veux dire par (SIGNAUX D'ENTREE): qui est un groupe de X dans la Figure 3 ?
Je veux dire les entrées ou les propriétés, mais quelles pourraient être les entrées ou les propriétés ? X3, X2 et X1 sont l'espace des caractéristiques d'entrée, et ce sont les images qui contiennent les caractéristiques que nous apprenons à classer. Par exemple, si nous donnons au modèle l'image d'un chat et lui disons que c'est un chat, et aussi nous lui donnons l'image d'un chien et lui disons que c'est un chien. Les entrées seront une image d'un chat et une image d'un chien, et bien sûr les images contiendront des caractéristiques telles que la forme du chat ou du chien ou sa couleur ou etc. Chacun a des caractéristiques qui le distinguent, et c'est ce que le modèle apprendra.

B- Que veux dire par (POIDS : synaptic weights) dans l'image ci-dessus
Les poids sont des valeurs aléatoires attribuées à chaque entrée x. Cela signifie que chaque X (propriété) a sa propre valeur de poids. Et nous savons que la valeur de x nous avons des informations car ce sont les images.
C- Que veut dire la JONCTION DE SOMMATION ∑, ou elle est appelée dans de nombreux livres comme (ENTRÉES PONDÉRÉES OU ACTIVATION DE SOMMATION) ?

En bref, cela signifie que nous multiplions chaque x par la valeur de w qui lui est associée, puis que nous les additionnons. signifie  x₁*w_k1 + x₂*w_{k2 + ... +}  et ainsi de suite et le signe signifie leur somme. Et le biais le considère actuellement comme une valeur de poids normale, et c'est ainsi que nous le traitons par programme. Le signe de multiplication signifie ici produit scalaire. Et le produit scalaire détermine le degré de similitude entre la valeur de w et x, ou en d'autres termes, quelle est la valeur de w proche de x. Parce que, comme nous l'avons mentionné, nous voulons que le modèle apprenne la valeur de w afin de la maintenir aussi proche que possible de la vraie valeur de x pendant la période d'apprentissage. Et la raison ? Pour qu'il sache comment classer toute nouvelle image en fonction des valeurs des poids qu'il a appris. Bien sûr, le résultat de cette multiplication me donne y comme nous le voyons dans l'équation, et y est l'étiquette que notre modèle attend, ou en d'autres termes, le résultat de la multiplication, le produit scalaire, est l'attente du modèle.
Bien sûr, au début w sera des valeurs aléatoires, donc l'étiquette attendue par le modèle sera une erreur. Je veux dire, vous pouvez lui donner une photo d'un chat et il dit que c'est une photo d'un chien. Je veux dire si l'image que nous avons donnée au modèle était une image de chat et que son étiquette est nulle. Le modèle peut s'attendre à 1. Voici le rôle de la fonction d'erreur, et calculons la différence d'erreur entre l'étiquette réelle de l'image et l'étiquette attendue par notre modèle. Après avoir calculé le taux d'erreur, le modèle ira mettre à jour la valeur de w via le gradient décent, et c'est ce qu'on appelle la rétropropagation, et ainsi de suite jusqu'à ce que nous rendions le taux d'erreur aussi proche que possible de zéro.
Qu'est-ce qu'on entends par (FONCTION D'ACTIVATION) ?

Considérez-le comme un déclencheur si une certaine condition est remplie dans le Perceptron. Nous avons de nombreux types différents de (fonctions d'activation), que nous expliquons comme suit :

Nous allons prendre un exemple pour montrer comment cela fonctionne.
Un exemple pour illustrer l'idée.
Si la sortie de l'un des neurones est x = 0,5. Par exemple, si nous utilisons la fonction d'activation n ° 1 des types ci-dessus dans la figure ci-dessus. Sur la base de notre exemple, la sortie sera 1 car 0,5, qui est la valeur de x supérieure à zéro, et si la valeur de x est égale à -0,8, par exemple, la sortie sera zéro, et ainsi de suite. La photo n ° 4 est le modèle que nous voulons construire et, comme nous l'avons mentionné, elle représente la ligne de la photo de gauche sur la photo N°1.
Maintenant que nous avons couvert les bases en détail. Comme nous l'avons mentionné plus tôt, nous allons vous mentionner les étapes impliquées dans tout modèle d'apprentissage en profondeur. Maintenant, nous allons vous donner un résumé de la façon de former n'importe quel modèle d'une manière simple et étape par étape.
Les étapes les plus courantes pour tout modèle d'apprentissage en profondeur :
Initialisez les poids : il peut être aléatoire ou il peut s'agir de zéros, et dans notre exemple, nous allons en faire des zéros, comme nous le voyons dans l'image suivante :

Maintenant, nous allons retirer le produit scalaire, ce qui signifie que nous allons multiplier les entrées, et c'est x, et nous avons les images dans les poids, qui sont les valeurs aléatoires. Ok, chaque image telle que x0 a un ensemble de propriétés et est constituée de nombres, nous aurons donc quelque chose comme l'image suivante :

Et puis nous le multiplions exactement comme nous l'avons vu dans l'image ci-dessus, donc le résultat sera le suivant :

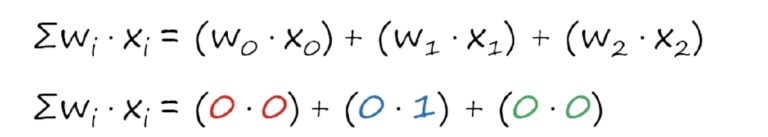
Choix de la fonction d'activation comme sur la photo n°4 : Dans notre exemple, nous allons utiliser une fonction très simple, la suivante :

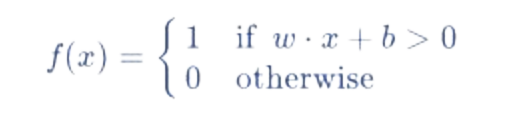
Le même que que nous venons d'expliquer il y a un moment. Si la condition est remplie, cela nous donne 1, et si elle n'est pas remplie, cela nous donne un zéro. La raison en est que nous avons mentionné dans notre exemple que nous avons des chats ou des chiens, nous les symboliserons donc, zéro ou un.

Fonction de coût : Ici, la fonction d'erreur est simple et c'est le résultat de l'étape ci-dessus. Si elle est nulle et que la vraie valeur de l'étiquette est également nulle, alors la prédiction est correcte et ainsi de suite pour tous les échantillons. Alors, que se passe-t-il si la prédiction est fausse ? Ici, nous devons mettre à jour et ajuster le processus connu sous le nom de rétropropagation
Rétropropagation : Ici, nous mettons à jour le poids jusqu'à ce que nous atteignions la valeur réelle dans l'étiquette, comme nous le verrons dans le prochain article. L'équation de mise à jour est la suivante :

Où le nouveau poids sera égal à l'ancien poids en plus du taux d'apprentissage, et nous le multiplions par la chose attendue par notre modèle, au cas où il s'agirait d'une erreur moins la valeur réelle de l'étiquette, et nous le multiplions par le propriété. Nous répétons l'étape jusqu'à ce que nous arrivions à la solution.